The Functor of Points

a fully faithful embedding

Morita Theory and Reconstruction

2 Comments Posted by on August 18, 2015

Given a “non-linear” object it is often useful to study various “linear” objects attached to it. For instance, given a ring R, we get the category of R-modules by letting R act on an abelian group. Given a group G, we get linear representations of G by letting G act on vector spaces. Given a space X, we can study vector bundles on X, or more generally, sheaves of abelian groups on X. In all of these examples, the collection of linear objects forms a category with very nice properties. A natural question is how much information is lost in this procedure. That is, to what extent can we recover an object from its linearization?

In this post we are going to talk about Morita equivalence from the perspective of reconstruction. Morita theory is most naturally discussed for non-commutative rings, although we will see that it has interesting consequences even for commutative rings. So, for the rest of this post, I will use “ring” to mean “not-necessarily commutative ring.”

Given the abstract abelian category R\text{-mod}, how would we go about reconstructing R? Well, R considered as a module over itself is an element of R\text{-mod}. We can recover the ring R by taking the endomorphisms of the module R. So, we just need to find a way to pick out the module R from all other R-modules. One way to do this would be to find a categorical property of R that uniquely determines it up to isomorphism of R-modules. However, this is actually impossible to do! The reason is that R\text{-mod} might have nontrivial automorphisms. Suppose that R is commutative. Then, if L is an invertible R-module, the map M\mapsto M\otimes L preserves the abelian category structure, and hence gives rise to a functor from R\text{-mod} to itself, which has an inverse given by tensoring with L^{-1}. Moreover, this map sends R to L, so any categorical property that R has L must have as well. So, it is impossible to identify the module R if we are given the abstract abelian category of R-modules. The best we can hope for is to find an invertible R-module. Of course, this isn’t actually a problem for us, because the endomorphism ring is a categorical construction! That is, we can recover the ring R by taking the endomorphism ring of any invertible R-module.

So, what categorical property does R, and hence all other invertible R-modules, have? It turns out the right observation is that it is a compact projective generator. Each of these properties is a condition on the functor \text{Hom}(c,-). As introduced in this post, an object c in a category C is compact if \text{Hom}(c,-) commutes with filtered colimits. It is projective if \text{Hom}(c,-) is exact, that is, if it commutes with finite colimits. We say that c is a generator if \text{Hom}(c,-) is faithful, that is, it is injective on morphisms.

Be careful: in this post, I defined a generator in a different way, using coproducts. These definitions are different in general, although they are closely related for cocomplete abelian categories. My excuse for this is that there are a lot of non-equivalent notions of a generator of a category. In fact, in this post, Qiaochu Yuan presents at least nine different definitions and analyzes their relations in detail.

In our situation, each of these properties is trivial to verify, because \text{Hom}(R,-) is just the identity functor. An arbitrary colimit can be written as a combination of filtered colimits and finite colimits. So, another way to phrase being a compact projective generator is that \text{Hom}(c,-) is faithful and commutes with all colimits.

How do we use these properties? Well, given any object M in any abelian category A, we can take the endomorphism ring R=\text{End}(M). For any object N in A, the abelian group \text{Hom}_A(M,N) has a natural R-module structure given by composition on the left. That is, the covariant Yoneda embedding A\hookrightarrow\text{Func}(A,\text{Ab}) factors through the forgetful functor R\text{-mod}\rightarrow\text{Ab}. It turns out that being a compact projective generator is exactly the condition we need for the functor \text{Hom}(M,-):A\rightarrow R\text{-mod} to be an equivalence of categories.

Proposition 1:
If M is an object in an abelian category A, then the functor \text{Hom}(M,-):A\rightarrow R\text{-mod} is an (additive) equivalence of categories if and only if M is a compact projective generator.
Proof
Suppose that M is a compact projective generator. As M is projective, taking cokernels shows that \text{Hom}(M,-) is full. It is faithful by definition of generator. To see that it is essentially surjective, take an R-module N. We can write N as a colimit over a diagram involving sums of copies of R. But, R=\text{Hom}(M,M), and \text{Hom}(M,-) is surjective on morphisms, so we can find a diagram in A that gets sent by \text{Hom}(M,-) to our chosen diagram. As \text{Hom}(M,-) commutes with colimits, we see that N is the image of the colimit of the diagram in A under \text{Hom}(M,-).Conversely, if \text{Hom}(M,-) is an equivalence, it must commute with arbitrary colimits and be faithful.

\square

In fact, every equivalence arises in this way.

Theorem 2:
Let A be a cocomplete abelian category, and R a (possibly non-commutative) ring. The covariant Yoneda embedding A\hookrightarrow\mbox{Func}(A,R\text{-mod}) restricts to an equivalence of categories

\{\mbox{Compact projective generators in }A\}\rightarrow\{\mbox{Additive equivalences of categories }A\to R\text{-mod}\}
Proof
Consider an additive equivalence F:A\rightarrow R\text{-mod}. There must then be an object M\in A such that F(A)\cong R. Because F is invertible, M is a compact projective generator. As F is additive, we have an isomorphism of rings \text{End}(M)\cong R. Take an element N\in A. Because M is a generator, we can find an epimorphism f:\oplus_iM\rightarrow N. This realizes M as the coequalizer of a pair of maps from \ker f to \oplus_iM. Surjecting onto the kernel again by a sum of copies of M, we may write N as the coequalizer of a diagram whose objects are sums of copies of M. But F and \text{Hom}(M,-) agree on M, which shows that F and \text{Hom}(M,-) are isomorphic as functors. This gives essential surjectivity of the above map. It is fully faithful by the covariant Yoneda lemma.

\square

We can deduce from this theorem a fact about commutative rings.

Corollary 3:
If R is a commutative ring, then the group of R-linear autoequivalences of R\text{-mod} is exactly \text{Pic} R.
Proof
Given any invertible R-module M, we get an R-linear autoequivalence of R\text{-mod}, and moreover these autoequivalences are all distinct for different isomorphism classes of M. Conversely, suppose F is an R-linear autoequivalence of R\text{-mod}. By Theorem 2, F is of the form \text{Hom}(M,-) for some compact projective generator M of R\text{-mod}. We also have the additive functor -\otimes M from R\text{-mod} to itself. It follows formally from the hom-tensor adjunction and the fact that \text{Hom}(M,-) is invertible that -\otimes M must be the inverse of \text{Hom}(M,-). In particular

M\otimes\text{Hom}(M,R)\cong R

and therefore M is an invertible module.

\square

The restriction to R-linear autoequivalences is not very important. It is just to rule out those autoequivalences of R\text{-mod} arrising from automorphisms of R. Indeed, one can show that the full (additive) auotequivalence group of R\text{-mod} is \text{Aut} R\ltimes\text{Pic} R.

Lets return to the problem of reconstructing R from R\text{-mod}. We cannot hope to recover R in general. The reason for this is that there are more compact projective generators in R\text{-mod} than just invertible modules. For instance, R^{\oplus n} is a compact projective generator, and more generally a finite direct sum of invertible modules is too. These objects give us equivalences of R\text{-mod} with S\text{-mod} for various rings S that are not isomorphic to R. In this case we say that R is Morita equivalent to S. For instance, \text{End}_R(R^{\oplus n})\cong M_n(R), so there is an equivalence of abelian categories between R\text{-mod} and M_n(R)\text{-mod} for any ring R. We can, however, always recover the center of R from R\text{-mod}. In particular, commutative rings are determined up to isomorphism by their module categories. To prove this, we make the definition:

Definition 1:
The center Z(C) of a category C is the endomorphism monoid of the identity functor C\rightarrow C.

If C is an additive category, then Z(C) carries a natural additive structure which makes it into a ring.

Proposition 4:
If R is a ring, then Z(R\text{-mod})=Z(R) (as rings).
Proof
We can think of the identity functor from R\text{-mod} to itself as \text{Hom}(R,-). By Theorem 2, the endormorphism ring of the functor \text{Hom}(R,-) is the same as the endomorphism ring of R as an R-module. But this is just Z(R).

\square

From the perspective of schemes, we can interpret this as saying that an affine scheme can be uniquely identified among all other affine schemes by its category of quasi-coherent sheaves. When we phrase it this way, an obvious question to ask is if this is true for general schemes. The answer is (almost) yes!

Theorem 5:[Gabriel]
If X and Y are quasi-separated schemes, then \text{Qcoh(X)}\cong\text{Qcoh}(Y) (as additive categories) implies X\cong Y.

You can find the proof of this theorem in the paper “Rosenberg’s Reconstruction Theorem (after Gabber)” by Martin Brandenburg. It turns out that the analog of Corollary 1 also continues to hold:

Theorem 6:
If X is a quasi-separated scheme, then the automorphism group of \text{Qcoh}(X) (as a linear category over X) is \text{Pic}(X).

If we remember the tensor structure as well, something really nice happens. It turns out that every cocontinuous monoidal functor \text{Qcoh}(X)\rightarrow\text{Qcoh}(Y) arrises as the pushforward map along a uniquely determined morphism f:X\rightarrow Y. In other words, we get an embedding of the category of (qcqs) schemes into some 2-category of abelian categories. So, all of the information contained in the category of schemes is also in their categories of quasicoherent sheaves!

Now, this is both good and bad news. On the one hand, this means that we can prove things about schemes by thinking about certain abelian categories. These categories have very nice properties, so this might be a useful tool. This also opens the door to various notions of generalized schemes. However, if we want to think of \text{Qcoh}(X) as being an invariant of X, this reconstruction theorem is bad news! Indeed, this invariant is just isomorphy, which is completely useless. A successful invariant should remember enough about the scheme to be interesting, but not too much so as to be completely uncomputable. The fix is to judiciously forget some information in \text{Qcoh}(X), but not too much. For instance, one can consider the bounded derived category D^b(X) of coherent sheaves on X. Studying the extent to which D^b(X) determines X is a big area of research nowadays.

Uncategorized

2 responses to “Morita Theory and Reconstruction”

  1. Qiaochu Yuan August 18, 2015 at 1:54 am

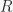    You say your rings are not necessarily commutative, but in the third paragraph you use a tensor product operation on modules and talk about invertible modules, which requires commutativity. For finding automorphisms of \text{Mod}(R) you want to look at not invertible R-modules but invertible (R, R)-bimodules.

    Like

    Reply

Leave a comment